GTK+ で落書き 12（Ruby）

三角形の内心・外心・重心・垂心・傍心
自分で求めた公式を使って、三角形の内接円と外接円を Ruby で描いてみました。
　

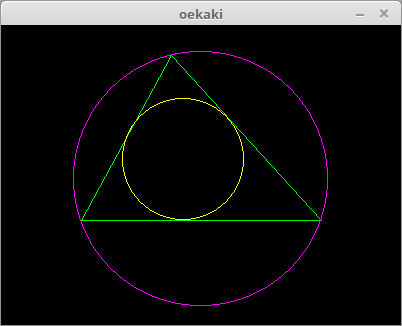
描画には自作の Gem 'oekaki' を使っています。
oekaki | RubyGems.org | your community gem host
GTK+でお絵かきしてみた（Ruby） - Camera Obscura

require 'oekaki'
require 'ostruct'

Width, Height = 400, 300

A = Vector[-0.2,  0.8]
B = Vector[-0.8, -0.3]
C = Vector[ 0.8, -0.3]

incircle     = OpenStruct.new
circumcircle = OpenStruct.new

l, m, n = (B - A).norm, (C - B).norm, (A - C).norm
q = l + m + n

incircle.p = A * (m / q) + B * (n / q) + C * (l / q)
incircle.r = sqrt((q / 2 - l) * (q / 2 - m) * (q / 2 - n) * 2 / q)

a = A[0] * (B[1] - C[1]) + B[0] * (C[1] - A[1]) + C[0] * (A[1] - B[1])

circumcircle.p = Vector[(A.norm ** 2 * (B[1] - C[1]) + B.norm ** 2 * (C[1] - A[1]) +
                            C.norm ** 2 * (A[1] - B[1])) / a,
                        (A.norm ** 2 * (C[0] - B[0]) + B.norm ** 2 * (A[0] - C[0]) +
                            C.norm ** 2 * (B[0] - A[0])) / a] / 2
circumcircle.r = (A - circumcircle.p).norm

class Vector
  def to_w
    l = Height / 2
    Vector[Width / 2 + self[0] * l, l - self[1] * l]
  end
end


Oekaki.app width: Width, height: Height do
  draw do
    clear
    
    color(0, 65535, 0)
    line(A.to_w[0], A.to_w[1], B.to_w[0], B.to_w[1])
    line(C.to_w[0], C.to_w[1], B.to_w[0], B.to_w[1])
    line(A.to_w[0], A.to_w[1], C.to_w[0], C.to_w[1])
    
    color(65535, 65535, 0)
    circle(false, incircle.p.to_w[0], incircle.p.to_w[1], incircle.r * Height / 2)
    
    color(65535, 0, 65535)
    circle(false, circumcircle.p.to_w[0], circumcircle.p.to_w[1],
       circumcircle.r * Height / 2)
  end
end

　
定数 A, B, C が三角形の頂点の座標なので、いろいろ変えて遊んでみて下さい。例えば

A = Vector[-0.7,  0.6]
B = Vector[-0.2, -0.8]
C = Vector[ 0.7, -0.4]

にすると

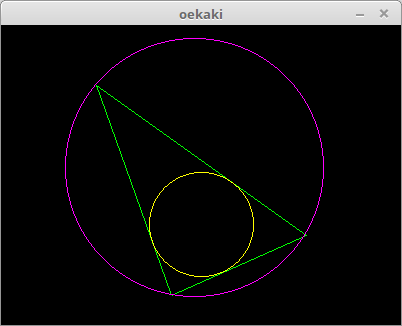
となります。ちなみに座標はウィンドウのそれではなく、原点がウィンドウの中心となるようなふつうの x-y座標系で、Y方向の最大最小値がそれぞれ 1, -1 になっています。

なお、Gem 'oekaki' のバージョンを 0.1.1 に上げました。変更点はメソッド Tool#clear の引数を省略した場合、黒色で画面クリアが行われるようにしたことです。上のコードはそれを前提に書かれています。
　

追記

こんなのも描いてみました。コードは下。
移動する内接円 · GitHub