L-system って何でしょうか。Wikipedia にはこうあります。
L-system(エルシステム、Lindenmayer system)は形式文法の一種で、植物の成長プロセスを初めとした様々な自然物の構造を記述・表現できるアルゴリズムである。自然物の他にも、反復関数系(Iterated Function System; IFS)のようないわゆる自己相似図形やフラクタル図形を生成する場合にも用いられる。
https://ja.wikipedia.org/wiki/L-system
つまりは、再帰曲線を描く言語ですね。例としてまず「コッホ曲線」を描いてみましょう。
まず、前に一定の長さ進むコマンドを「F」とします。で、開始手続きも「F」としましょう。これだけで
と直線が一本引かれます。
つぎに、再帰的な「置き換え」の規則を定めます。それを「F→F-F++F-F」とします。これは開始手続きの「F」を「F-F++F-F」で置き換えるということになります。「-」は左60度、「+」は右60度の回転とします。よって、新たな手続きも「F-F++F-F」となります。これを図示すると
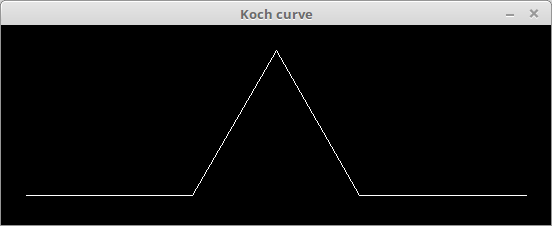
となります。
置き換えを続けましょう。今度は前の手続き「F++F-F」の F をすべて F++F-F に置き換えます。すると「F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F」となります(ややこしいですね)。これは
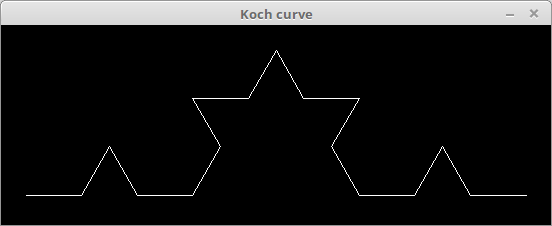
となります。
もう一度置き換えてみます。今度は「F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F-F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F-F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F」ですよ。これは
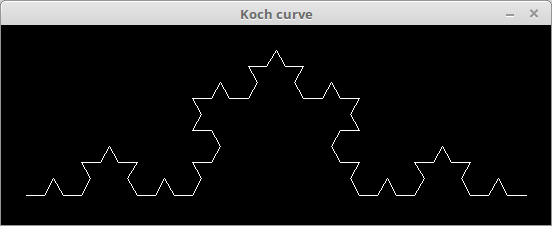
となりますね。まさしく再帰的な「コッホ曲線」が描けています。
さて、これはこんなコードで描けます。Gem化しているので、Gem 'kaki-lsystem' をインストールして下さい。
require 'kaki/lsystem' n = 3 length = 500.0 / 3 ** n l = Lsystem.new(550, 200) l.move(-250, -70) l.set("-") {left(60)} l.set("+") {right(60)} l.set("F") {forward(length)} l.init("F") l.rule("F", "F-F++F-F") l.draw(n)
init("F") は開始手続きの指定、rule("F", "F-F++F-F") は置き換えの規則の指定です。draw(3) で変換を 3回施したものを描画します。
set("-") {left(60)} はコマンド「-」が何をするのか、ブロック内に記述します。つまり left(60) は左60度回転ということですね。forward(20) ならまっすぐ 20 進むということです(ちなみに forward(20, false) なら、描画せずに 20 進みます)。このブロック内は、じつは Gem 'oekaki' のタートルグラフィックスの機能を使っているので、そのメソッドを書きます。よく使うのは left(deg), right(deg), forward(length, draw=true) あたりでしょうか。これについては
- タートルグラフィックスで再帰曲線をいろいろ描いてみる(Ruby) - Camera Obscura
- File: README — Documentation for kaki-lsystem (0.0.3)
などを参考にして下さい。なお、set() は使用したすべてのコマンドについて設定して下さい。何もしない場合でも空のブロックが必要です。また、rule() で変換規則が指定されていないコマンドは、そのまま持ち越されます。
置き換えるコマンドを二種類以上にすることもできます。例えば
require 'kaki/lsystem' l = Lsystem.new(400, 350, "Dragon curve") l.move(-50, -50) l.prologue do clear(color(0xf7d3, 0xffff, 0xc99b)) #背景色 color(0x143f, 0x832d, 0xe783) #ペンの色 end l.set("-") {left(90)} l.set("+") {right(90)} l.set("A") {forward(20)} l.set("B") {forward(20)} l.init("A") l.rule("A", "A+B+") l.rule("B", "-A-B") l.draw(7)
では、開始手続きが A で、置き換えの規則は「A→A+B+」「B→-A-B」と二種類になっています。これを実行すると
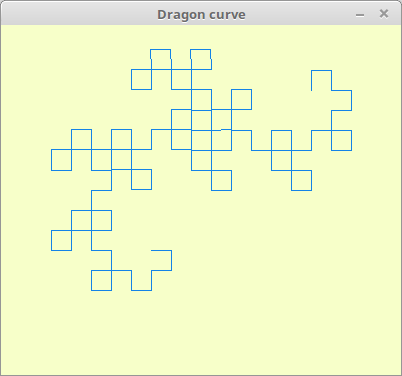
となります。いわゆる「ドラゴン曲線」ですね。他のメソッドも簡単に説明しておきましょう。move(x, y) はペンの開始位置を指定します。デフォルトは (0, 0) で、これはキャンバスの中心です。なお、数学のグラフと同じで y方向は上がプラスの向きです。prologue {...} はブロック内で初期処理をします。背景色や色の指定をすることが多いです。なお、ここでは残念ながら left(), right() が使えない(というか2度呼ばれてしまうので正確に指定できません)ので、ペンの最初の方向はアクセサーメソッド dir= で指定することになります(あとで説明します)。
コマンド「[」「]」でスタックのプッシュ、ポップを表します。つまり [ で状態を保存し、 ] で元の状態に復帰します。例えば
require 'kaki/lsystem' l = Lsystem.new(400, 640) l.move(50, -310) l.prologue {color(0x28a5, 0xa3c8, 0xca7)} l.dir = Vector[0, 1] l.set("-") {left(15)} l.set("+") {right(15)} l.set("F") {forward(10)} l.init("F") l.rule("F", "F[+F-F-F]F[--F+F+F]") l.draw(4)
こんな風です。dir= で開始時の方向をベクトルで指定しています。ただし、ベクトルは単位ベクトル(長さが 1 )になるようにして下さい。この結果は



となります。左からそれぞれ 1, 2, 4 回の繰り返しになります。
ブロックはクロージャなので、変数を使ったサンプル。「ヒルベルト曲線」の色を描画しながら替えていきます。
require 'kaki/lsystem' n, f = 0, 0 col = [[0xffff, 0, 0], [0, 0xffff, 0]] l = Lsystem.new(500, 500, "Hilbert curve") l.move(-230, 230) l.set("+") {left(90)} l.set("-") {right(90)} l.set("A") {} l.set("B") {} l.set("F") do if n.zero? f = (f + 1) % 2 color(*col[f]) end forward(15) n = (n + 1) % 16 end l.init("A") l.rule("A", "-BF+AFA+FB-") l.rule("B", "+AF-BFB-FA+") l.draw(5)
Gem 'kaki-lsystem' のソースコードは Gist にあります。この Gem は内部で Gem 'oekaki' を使っています。
https://gist.github.com/obelisk68/1c3d278cb5fe2778a11ba719d44af743
※参考にしたページ(ありがとうございます!)
L-system
L-system入門 - 人工知能に関する断創録
HiiragiCompany -L-System Tips-
L-systemを利用した植物の描画 | Makoto Hirahara
※L-system の描画例
obelisk.hatenablog.com
