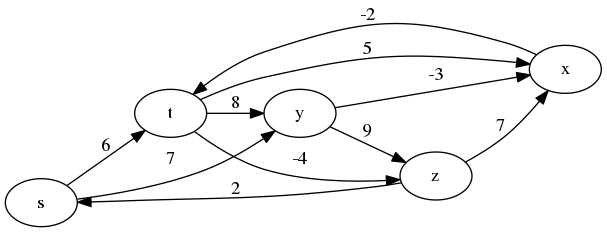
ベルマン−フォード・アルゴリズム（Ruby）

ベルマン−フォード・アルゴリズムは、ダイクストラ法にさらに辺の重みが負の場合も含めて最短経路を求めることができます。入出力などはダイクストラ法の場合を参照して下さい。

コーディングは Ruby で行いました。返り値は配列 [shortest, pred] で、pred を見ると最短経路がわかります。
bellman_ford.rb

def bellman_ford(g, s)
  h = g.map {|x| [x[0], x[1].keys]}.to_h
  
  shortest = Hash.new(Float::INFINITY)
  pred = {}
  
  shortest[s] = 0
  
  (h.size - 1).times do
    h.each do |k, v|
      v.each do |x|
        if (a = shortest[k] + g[k][x]) < shortest[x]
          shortest[x] = a
          pred[x] = k
        end
      end
    end
  end
  
  [shortest, pred]
end

if __FILE__ == $0
  g = {s: {t: 6, y: 7}, t: {x: 5, y: 8, z: -4},
       x: {t: -2}, y: {z: 9, x: -3}, z: {s: 2, x: 7}}
  p bellman_ford(g, :s)
end
#=>[{:s=>0, :t=>2, :y=>7, :x=>4, :z=>-2}, {:t=>:x, :y=>:s, :x=>:y, :z=>:t}]

ベルマン−フォード・アルゴリズムは負の閉路を検出できます。下の find_negative_weight_cycle メソッドで、負の閉路がない場合は空の配列を、ある場合は閉路の頂点の順番を配列で返します。

def find_negative_weight_cycle(g, s)
  shortest, pred = bellman_ford(g, s)
  
  g.each do |u, v1|
    v1.each_key do |v2|

      if shortest[u] + g[u][v2] < shortest[v2]
        visited = Hash.new(false)
        x = v2
        until visited[x]
          visited[x] = true
          x = pred[x]
        end
        
        v = pred[x]
        cycle = [x]
        until v == x
          cycle.unshift(v)
          v = pred[v]
        end
        return cycle
      end
      
    end
  end
  []
end

if __FILE__ == $0
  g = {s: {t: 6, y: 7}, t: {x: 5, y: 8, z: -4},
       x: {t: -2}, y: {z: 9, x: -3}, z: {s: 2, x: 7, y: 1}}
  p bellman_ford(g, :s)
  p find_negative_weight_cycle(g, :s)
end
#=>[{:s=>-4, :t=>-2, :y=>-5, :x=>-4, :z=>-6}, {:t=>:x, :y=>:z, :x=>:y, :z=>:t, :s=>:z}]
#=>[:z, :y, :x, :t]