ダイクストラ法（Ruby）

前エントリでは閉路なし有向グラフ（DAG）の場合に最短経路を求めてみましたが、ダイクストラ法は閉路があり、かつ辺の重みが非負の場合に最短経路を求めることができます。入出力は、閉路があって辺の重みが非負である以外、DAG の場合と同じなので、そちらを見て下さい。

コーディングは Ruby で行いました。返り値は配列 [shortest, pred] で、pred を見ると最短経路がわかります。
dijkstra.rb

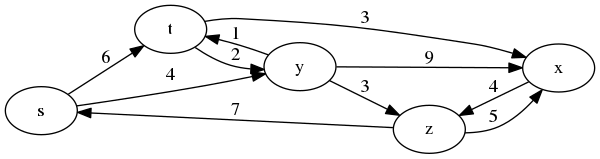
def dijkstra(graph, start)
  h = graph.map {|x| [x[0], x[1].keys]}.to_h
  
  shortest = Hash.new(Float::INFINITY)    #デフォルトは充分大きな数
  pred = {}
  done = h.keys.map {|node| [node, false]}.to_h
  
  shortest[start] = 0
  
  loop do
    #確定していない中でスタート地点から最短のノードを探す（u）
    u = nil
    h.each_key.reject {|node| done[node]}.each do |node|
      u = node if !u or shortest[node] < shortest[u]
    end
    break unless u
    done[u] = true    #探されたuは確定
    
    #ノードuから行けるノードvまで、スタート地点からuを経由した方が短ければshortest[v]を更新する
    h[u].each do |v|
      if (a = shortest[u] + graph[u][v]) < shortest[v]
        shortest[v] = a
        pred[v] = u
      end
    end
  end
  
  [shortest, pred]
end

if __FILE__ == $0
  graph = {s: {t: 6, y: 4}, t: {x: 3, y: 2},
           x: {z: 4}, y: {z: 3, t: 1, x: 9}, z: {s: 7, x: 5}}
  p dijkstra(graph, :s)
end
#=>[{:s=>0, :t=>5, :y=>4, :z=>7, :x=>8}, {:t=>:y, :y=>:s, :z=>:y, :x=>:t}]