トポロジカルソート（Ruby）

　
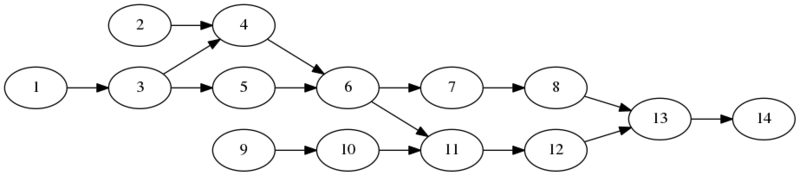
閉路なし有向グラフ（DAG: directed acyclic graph）のトポロジカルソートです。トポロジカルソートとは、上のようなグラフがあったとき、

入力：1〜n の頂点をもつ閉路なし有向グラフ。
出力：グラフ内の辺を (u, v) とするとき、u が v の前になるように並べられた頂点の線形順序。

となる手続きのことです。

Ruby でコーディングしました。有向グラフはハッシュで実装しています（隣接リスト）。なので、頂点の数 n は特に与える必要はなくなっています。
topological_sort.rb

class Hash
  def topological_sort
    #%node = Object
    #Hash{self[%node]: %node} -> Hash{in_degree[%node]: Integer}, %node{u, ans[], nxt[]}
    
    in_degree = Hash.new(0)
    ans = []
    
    each_value do |v|
      v.each {|x| in_degree[x] += 1}
    end
    
    nxt = keys.select {|x| in_degree[x].zero?}
    
    until nxt.size.zero?
      u = nxt.shift
      ans << u
      self[u].each do |v|
        in_degree[v] -= 1
        nxt << v if in_degree[v].zero?
      end
    end
    raise "グラフに閉路があります。" if in_degree.values.find {|x| not x.zero?}
    
    ans
  end
end

if __FILE__ == $0
  g = {1=>[3], 2=>[4], 3=>[4, 5], 4=>[6], 5=>[6], 6=>[7, 11],
       7=>[8], 8=>[13], 9=>[10], 10=>[11], 11=>[12], 12=>[13],
       13=>[14], 14=>[]}
  p g.topological_sort
end
#=>[1, 2, 9, 3, 10, 4, 5, 6, 7, 11, 8, 12, 13, 14]

なお、頂点にはじつはどのようなオブジェクトを使うこともできます。

g = {1=>[3], 2=>["4"], 3=>["4", 5], "4"=>[6], 5=>[6], 6=>[7, 11],
     7=>[8], 8=>[:a], 9=>[10], 10=>[11], 11=>[12], 12=>[:a],
     :a=>[14], 14=>[]}
p g.topological_sort
#=>[1, 2, 9, 3, 10, "4", 5, 6, 7, 11, 8, 12, :a, 14]

　
有向グラフの実装としては、隣接リスト以外に「隣接行列」という表し方もあります。
　

アルゴリズムの基本

　

追記

Hash クラスへのモンキーパッチでないように書き換えました。(2019/5/6)

def topological_sort(g)
  in_degree = Hash.new(0)
  ans = []
  
  g.each_value do |v|
    v.each {|x| in_degree[x] += 1}
  end
  
  nxt = g.keys.select {|x| in_degree[x].zero?}
  
  until nxt.size.zero?
    u = nxt.shift
    ans << u
    g[u].each do |v|
      in_degree[v] -= 1
      nxt << v if in_degree[v].zero?
    end
  end
  raise "グラフに閉路があります。" if in_degree.values.find {|x| not x.zero?}
  
  ans
end


if __FILE__ == $0
  g = {1=>[3], 2=>[4], 3=>[4, 5], 4=>[6], 5=>[6], 6=>[7, 11],
       7=>[8], 8=>[13], 9=>[10], 10=>[11], 11=>[12], 12=>[13],
       13=>[14], 14=>[]}
  p topological_sort(g)
end
#=>[1, 2, 9, 3, 10, 4, 5, 6, 7, 11, 8, 12, 13, 14]