閉路なし有向グラフ（DAG）の最短経路（Ruby）

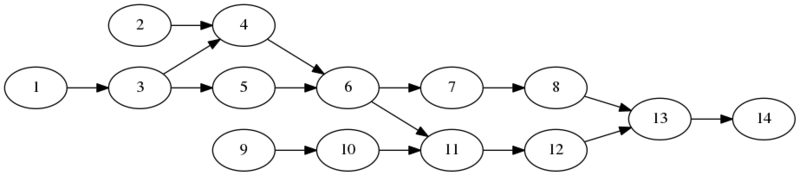
上の閉路なし有向グラフ（DAG）のように、辺に「重み」が付いている場合において、最短経路を求めてみます。手続きは

入力：

• G: n 個の頂点の集合 V と m 本の有向辺の集合 E を含む閉路なし有向グラフ。
• s: V の始点。

出力：

• V に含まれる始点以外の頂点 v について、@shortest[v] は s から v への最短経路重み sp(s, v) であり、@pred[v] は何らかの最短経路上で v の直前にある頂点である。始点では、@shortest[s] = 0, @pred[s] = nil であり、s から v へのパスがない場合、@shortest[v] = ∞, @pred[v] = nil である。

　
Ruby でコーディングしてみました。メソッドは [@shortest, @pred] を返します。@pred を見ると最短経路がわかります。
dag_shortest_paths.rb

require './topological_sort'

class Hash
  def dag_shortest_paths(s)
    #%dis = Rational or Integer or Float, %node = Object
    #Hash{self[%node]: (Hash[%node]: %dis)}, %node{s} ->
    #Hash{h[%node]: Array[%node], @shortest[%node]: %dis, @pred[%node]: %node}
    #%node{l[]}
    
    h = map {|x| [x[0], x[1].keys]}.to_h
    l = h.topological_sort
    
    @shortest = h.keys.map {|k| [k, Float::INFINITY]}.to_h
    @pred = {}
    
    @shortest[s] = 0
    
    l.each do |u|
      h[u].each {|v| relax(u, v)}
    end
    
    [@shortest, @pred]
  end
  
  def relax(u, v)
    #%node{u, v} --> %dis{a}
    if (a = @shortest[u] + self[u][v]) < @shortest[v]
      @shortest[v] = a
      @pred[v] = u
    end
  end
  private :relax
end

if __FILE__ == $0
  g = {s: {t: 2, x: 6}, t: {x: 7, y: 4},
       x: {y: -1, z: 1}, y: {z: -2}, z: {}}
  p g.dag_shortest_paths(:s)
end
#=>[{:s=>0, :t=>2, :x=>6, :y=>5, :z=>3}, {t=>:s, :x=>:s, :y=>:x, :z=>:y}]

topological_sort.rb は前エントリのコードです。ハッシュを使うとき、to_h 便利ですね。

念のため、返り値 @pred から最短経路を順に配列に入れて返すメソッドを書いておきます。

class Hash
  def get_order(a)
    #Hash{self[%node]: %node}, %node or nil{a} -> %node{order[]}
    order = []
    while a
      order.unshift(a)
      a = self[a]
    end
    order
  end
end

pred = {:t=>:s, :x=>:s, :y=>:x, :z=>:y}
p pred.get_order(:z)    #=>[:s, :x, :y, :z]

アルゴリズムの基本

　

追記

Hash クラスへのモンキーパッチでないように書き換えました。(2019/5/6)

def dag_shortest_paths(g, start)
  h = g.map {|x| [x[0], x[1].keys]}.to_h
  l = topological_sort(h)
  
  shortest = h.keys.map {|k| [k, Float::INFINITY]}.to_h
  pred = {}
  
  shortest[start] = 0
  
  l.each do |u|
    h[u].each do |v|
      if (a = shortest[u] + g[u][v]) < shortest[v]
        shortest[v] = a
        pred[v] = u
      end
    end
  end
  
  [shortest, pred]
end

def topological_sort(h)
  in_degree = Hash.new(0)
  ans = []
  
  h.each_value do |v|
    v.each {|x| in_degree[x] += 1}
  end
  
  nxt = h.keys.select {|x| in_degree[x].zero?}
  
  until nxt.size.zero?
    u = nxt.shift
    ans << u
    h[u].each do |v|
      in_degree[v] -= 1
      nxt << v if in_degree[v].zero?
    end
  end
  raise "グラフに閉路があります。" if in_degree.values.find {|x| not x.zero?}
  
  ans
end


if __FILE__ == $0
  g = {s: {t: 2, x: 6}, t: {x: 7, y: 4},
       x: {y: -1, z: 1}, y: {z: -2}, z: {}}
  p dag_shortest_paths(g, :s)
end
#=>[{:s=>0, :t=>2, :x=>6, :y=>5, :z=>3}, {t=>:s, :x=>:s, :y=>:x, :z=>:y}]

トポロジカルソート（Ruby）

　
閉路なし有向グラフ（DAG: directed acyclic graph）のトポロジカルソートです。トポロジカルソートとは、上のようなグラフがあったとき、

入力：1〜n の頂点をもつ閉路なし有向グラフ。
出力：グラフ内の辺を (u, v) とするとき、u が v の前になるように並べられた頂点の線形順序。

となる手続きのことです。

Ruby でコーディングしました。有向グラフはハッシュで実装しています（隣接リスト）。なので、頂点の数 n は特に与える必要はなくなっています。
topological_sort.rb

class Hash
  def topological_sort
    #%node = Object
    #Hash{self[%node]: %node} -> Hash{in_degree[%node]: Integer}, %node{u, ans[], nxt[]}
    
    in_degree = Hash.new(0)
    ans = []
    
    each_value do |v|
      v.each {|x| in_degree[x] += 1}
    end
    
    nxt = keys.select {|x| in_degree[x].zero?}
    
    until nxt.size.zero?
      u = nxt.shift
      ans << u
      self[u].each do |v|
        in_degree[v] -= 1
        nxt << v if in_degree[v].zero?
      end
    end
    raise "グラフに閉路があります。" if in_degree.values.find {|x| not x.zero?}
    
    ans
  end
end

if __FILE__ == $0
  g = {1=>[3], 2=>[4], 3=>[4, 5], 4=>[6], 5=>[6], 6=>[7, 11],
       7=>[8], 8=>[13], 9=>[10], 10=>[11], 11=>[12], 12=>[13],
       13=>[14], 14=>[]}
  p g.topological_sort
end
#=>[1, 2, 9, 3, 10, 4, 5, 6, 7, 11, 8, 12, 13, 14]

なお、頂点にはじつはどのようなオブジェクトを使うこともできます。

g = {1=>[3], 2=>["4"], 3=>["4", 5], "4"=>[6], 5=>[6], 6=>[7, 11],
     7=>[8], 8=>[:a], 9=>[10], 10=>[11], 11=>[12], 12=>[:a],
     :a=>[14], 14=>[]}
p g.topological_sort
#=>[1, 2, 9, 3, 10, "4", 5, 6, 7, 11, 8, 12, :a, 14]

　
有向グラフの実装としては、隣接リスト以外に「隣接行列」という表し方もあります。
　

アルゴリズムの基本

　

追記

Hash クラスへのモンキーパッチでないように書き換えました。(2019/5/6)

def topological_sort(g)
  in_degree = Hash.new(0)
  ans = []
  
  g.each_value do |v|
    v.each {|x| in_degree[x] += 1}
  end
  
  nxt = g.keys.select {|x| in_degree[x].zero?}
  
  until nxt.size.zero?
    u = nxt.shift
    ans << u
    g[u].each do |v|
      in_degree[v] -= 1
      nxt << v if in_degree[v].zero?
    end
  end
  raise "グラフに閉路があります。" if in_degree.values.find {|x| not x.zero?}
  
  ans
end


if __FILE__ == $0
  g = {1=>[3], 2=>[4], 3=>[4, 5], 4=>[6], 5=>[6], 6=>[7, 11],
       7=>[8], 8=>[13], 9=>[10], 10=>[11], 11=>[12], 12=>[13],
       13=>[14], 14=>[]}
  p topological_sort(g)
end
#=>[1, 2, 9, 3, 10, 4, 5, 6, 7, 11, 8, 12, 13, 14]

「既約分数クイズ」を解く（Ruby, C言語）

ここのところで結城先生の「既約分数クイズ」のことを知りました。結城先生らしい「お話」仕立てですので、是非参照して頂きたいですが、簡単にいうと

問題：正の整数Nが与えられているとき、 以下の条件を満たす既約分数p/qを「すべて」求めるアルゴリズムを示してください。 条件は：

• p, qは整数(pは0以上で、qは1以上N以下).
• gcd(p, q) = 1 (pとqの最大公約数は1).
• 0 <= p/q <= 1.

http://www.hyuki.com/dig/frac.html

というものです。

Ruby で解いてみたのですが、これだとあっさり解けすぎますよね。結城先生はもっと考えてごらんということだと思います。

N = 10
p (1..N).flat_map {|q| (0..q).map {|p| Rational(p, q)}}.uniq

結果。

[(0/1), (1/1), (1/2), (1/3), (2/3), (1/4), (3/4), (1/5), (2/5), (3/5), (4/5),
 (1/6), (5/6), (1/7), (2/7), (3/7), (4/7), (5/7), (6/7), (1/8), (3/8), (5/8),
 (7/8), (1/9), (2/9), (4/9), (5/9), (7/9), (8/9), (1/10), (3/10), (7/10), (9/10)]

まだあまり慣れていない C言語で書いてみましょう。
irreducible_fraction_problem.c

#include <stdio.h>
#include <stdlib.h>

int n = 10;

int gcd(int p, int q) {
    if (!q) return p;
    return gcd(q, p % q);
}

int main () {
    int *a;
    int co = 2;
    a = malloc(sizeof(int) * n * n);
    
    a[0] = 0;
    a[1] = 1;
    
    for (int q = 1; q <= n; q++) {
        for(int p = 1; p <= q; p++) {
            if (gcd(p, q) != 1) continue;
            a[co++] = p;
            a[co++] = q;
        }
    }
    
    for (int i = 0; i <= co - 2; i += 2) {
        printf("%d/%d ", a[i], a[i + 1]);
    }
    
    printf("\n");
    free(a);
    
    return 0;
}

結果。

0/1 1/1 1/2 1/3 2/3 1/4 3/4 1/5 2/5 3/5 4/5
1/6 5/6 1/7 2/7 3/7 4/7 5/7 6/7 1/8 3/8 5/8
7/8 1/9 2/9 4/9 5/9 7/9 8/9 1/10 3/10 7/10 9/10

　
こんなのでどうですかね。なお gcd(int p, int q) は「ユークリッドの互除法」を使って p と q の最大公約数を求めます。

なお、結城先生の「解答編」もあります。こちらもどうぞ。

フォードの円、GTK+ で落書き10（Ruby）

いわゆる「フォードの円」というものを描いてみました。これについてはここで知ったものです。ありがとうございます。

Ruby で描きました。描画には自作の Gem 'oekaki' を使っています。


oekaki_sample10.rb

require 'oekaki'

Width, Height = 500, 500

Oekaki.app width: Width, height: Height do
  draw do
    color(0, 0, 0)
    rectangle(true, 0, 0, Width, Height)
    
    color(0, 65535, 0)
    r = Width / 2
    circle(false, 0, r, r)
    circle(false, 2 * r, r, r)
    
    (1..9).to_a.combination(2) do |p, q|
      x = p / q.to_f
      y = 1 / (2 * q ** 2).to_f
      wx, wy = Width * x, Height * y
      circle(false, wx, Height - wy, wy)
    end
  end
end

　
Gem 'oekaki' についてはこちら。
oekaki | RubyGems.org | your community gem host
GTK+でお絵かきしてみた（Ruby） - Camera Obscura

　
なお、Gem 'oekaki' のバージョンを 0.0.11 に上げました。

Tool#ciecle と Tool#timer_stop の二つのメソッドを追加しました。circle(fill, x, y, r, color = nil) は円を arc メソッドよりも簡単に書けるようにしただけです。(x, y) は中心の座標、r は半径です。timer_stop(id) は Gtk.timeout_remove(id) のエイリアスに過ぎません。

基数ソート（Ruby）

基数ソートは固定長の文字列のソートなどに使うアルゴリズムで、下の位（文字列の右の方）から順にソートしていって、すべての位をソートし終えたとき、全体のソートが終っているという方法です。個々のソートには高速な「計数ソート」を使うとよい（「安定的な」ソートを使わねばなりません）。

Ruby でコーディングしてみました。
radix_sort.rb

class Array
  def counting_sort
    #Integer{a1[], s, m, equal[]}, String{a2[], result[]}
    
    a1, a2 = self[0], self[1]
    s = a1.size
    m = a1.max + 1
    equal = Array.new(m, 0)
    
    s.times {|i| equal[a1[i]] += 1}
    
    equal[-1] = 0
    (m - 1).times {|i| equal[i] += equal[i - 1]}
    
    result = Array.new(s)
    s.times do |i|
      result[equal[a1[i] - 1]] = a2[i]
      equal[a1[i] - 1] += 1
    end
    result
  end
  
  def radix_sort
    #String{self[]} -> Integer{ar[]} >> [String]
    st = self
    n = st[0].length
    n.times do |i|
      ar = st.map {|x| x[n - 1 - i].bytes[0]}
      st = [ar, st].counting_sort
    end
    st
  end
end

st = []
9.times {st << ("0".."9").to_a.sample(5).join}

p st
p st.radix_sort

実行例。

$ ruby radix_sort.rb
["24685", "74186", "81935", "17042", "74395", "72506", "52381", "78359", "10372"]
["10372", "17042", "24685", "52381", "72506", "74186", "74395", "78359", "81935"]

アルゴリズムの基本

バケットソート（と計数ソート）（Ruby）

バケットソートはバケツソート、ビンソート、計数ソート（後記：計数ソートとバケットソートはちがう）などとも言います。非常に高速ですが、ソートされる対象は 0以上の整数値（またはそれに変換できるもの）であり、その最大値が大きくなるとメモリをバカ食いします。また、値に重複がない場合はここにあるように Ruby では

class Array
  def bucket_sort
    inject([]) {|mem, var| mem[var] = var; mem}.compact
  end
end

と驚異的にシンプルに書けますが、値の重複を許すとそんなに簡単ではないようです。

バケットソートについては小飼弾さんのブログ記事が啓蒙的です。

参考書の手続きを Ruby でコーディングしてみました。値が重複する場合も対応しています。

class Array
  def counting_sort
    #Integer{self[]} -> Integer{m, equal[], result}
    m = max + 1
    equal = Array.new(m, 0)
    size.times {|i| equal[self[i]] += 1}
    
    equal[-1] = 0
    (m - 1).times {|i| equal[i] += equal[i - 1]}
    
    result = Array.new(size)
    size.times do |i|
      result[equal[self[i] - 1]] = self[i]
      equal[self[i] - 1] += 1
    end
    result
  end
end

やっていることは、値の最大値 + 1 を m として、まず大きさ m の配列 equal を作り、値 a の（重複する）要素の個数を equal[a] に入れます。つまり、ソートすべき配列に 4の値が 3個あれば、equal[4] = 3 とするということです。

次に、値 a より小さいすべての要素の個数を equal[a - 1] に入れます。

最後に並べ直します。ソートすべき配列と同じ大きさの配列 result を作り、ソートすべき配列の i 番目の値 a が result[equal[a - 1]] に入ります。重複したものが重ねて入らないように equal[a - 1] をインクリメントします。これをすべての i について繰り返すと、result に答えが入っています。

バケットソート計数ソートは上を見てわかるとおり、「値の比較」というものをまったくやっていません。それが高速になる理由です。

※追記　どうやらこのソートはバケットソートではなく、計数ソートというべきのようです。日本語版 Wikipedia は記述がまちがっているようだ。計数ソートとバケットソートは同じではないらしい。計数ソートは「安定的な」ソートです。つまり重複部分で、オブジェクトなど、付随するデータの順序を変えません。

アルゴリズムの基本

　

※追記
ぐぐっていたらもっとシンプルな実装を見つけました。多少好みの書き方に直して下に記しておきます。（後記：これはバケットソートなんでしょうか、よくわかりません。）

class Array
  def bucket_sort
    m = max + 1
    equal = Array.new(m, 0)
    size.times {|i| equal[self[i]] += 1}
    
    result = []
    m.times do |i|
      equal[i].times {result << i}
    end
    result
  end
end

後半でループがネストしているのでサイズが大きくなると不利かなと思いましたが、ベンチマークしてみると、サイズが小さくても大きくてもこちらの方が若干速いようです。何といってもシンプルなので、こちらの方がいいですね。

ただひとつ気になるのは、こちらの実装だとサテライトデータ（ソートに付随するデータ）が扱えないのではないでしょうか（つまり、「安定的な」ソートではない）。最初の実装はサテライトデータを扱うことが可能です。

マージソートとクイックソートの比較（Ruby）

自分の実装で、マージソートとクイックソートのベンチマークをしてみました。
マージソートの実装はこれ、クイックソートのはこれ（いちばん下の実装）です。
　
マージソート。

クイックソート。

基本的にクイックソートの方が速いようである。

ベンチマーク。
bench_sorts.rb

require 'benchmark'

100.times do
  ar = (0..10_0000).to_a.shuffle
  Benchmark.bm 12 do |x|
    x.report("merge sort") {ar.merge_sort}
    x.report("quick sort") {ar.qsort}
  end
end

実行は $ ruby bench_sorts.rb > bench_sorts.txt。

Gnuplot でグラフ化。

require 'histogram/array'
require 'numo/gnuplot'

ar = open("bench_sorts.txt", &:readlines)
m = []
q = []
ar.each_slice(3) {|x| m << x[1]; q << x[2]}

pick_up = proc do |ar|
  ar.each_with_object([]) {|i, a| a << i.split(" ")[6].to_f}
end

mb, mf = pick_up.call(m).histogram
qb, qf = pick_up.call(q).histogram

Numo.gnuplot do
  set title: "merge sort"
  set terminal: [png: {size: [400, 300]}]
  set output: 'sort_m.png'
  set style: [:fill, :solid, {border: -1}]
  plot mb, mf, w: :boxes, lc: {rgb: "orange"}
end

Numo.gnuplot do
  set title: "quick sort"
  set terminal: [png: {size: [400, 300]}]
  set output: 'sort_q.png'
  set style: [:fill, :solid, {border: -1}]
  plot qb, qf, w: :boxes, lc: {rgb: "orange"}
end